Анализ за фигури в равнини

louche 3 Точки

Анализ за фигури в равнини

Привет,

Математика изобщо меко казано не ми е от силните страни, не е била и няма да бъде, но не искам и да замахвам с лека ръка и поне да я "мъча", но единствено на всички задачи където за условие е дадено фигура Х в равнината, просто давам пълен блокаж.

Та срам не срам, макар да им имам решенията, което е различно от да съм ги разбрал, продължавам вече месеци да се чудя за тях, и тъй като в момента си преповтарям за "спорта" всички задачи... пак до тях стигнах:

тема 2, задача 8 - Лице на правоъгълник в равнината

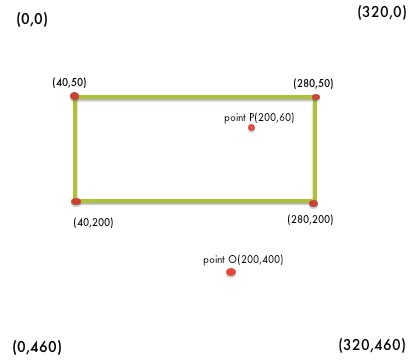
тема 4, задача 3 - Точка в правоъгълник

тема 4, задача 6 - Точка върху страната на провоъгълник

Ще може ли, ако не е проблем и на някой му се занимава, да се направи един пълен анализ на самите задачи и решенията им?

Благодаря.

Тагове:

19/01/2017 18:02:01 Module: Java Advanced 19/01/2017 19:08:10

ThePSXHive 436 Точки

Best Answer

Задачи с "фигура X в равнината" е събирателен термин за задачите в които е възможно разглеждането на двуизмерни обекти в една от две широко използвани 2-D координатни системи:

Координатната система в лявата страна на изображението се нарича Декартова (правоъгълна) координатна с-ма, докато координатната система вдясно на изображението е известна като инвертирана ("преобърната") к-на система. Първата е тази, с която повечето от нас са запознати, преди да започнат да се занимават с програмиране (и особено компютърна графика). Голяма част от съвременните компютърни платформи боравят с втория тип к-на система, като се имат предвид и множество мобилни устройства. Въпреки всичко, има изключения.

Информацията с която разполагаш в двете задачи, е разположението (координатите) на горния ляв и долния десен ъгъл на съответната двуизмерна фигура (правоъгълник, в случая); (x1, y1), и (x2, y2). Изразите за лице и периметър на правоъгълникът са едни и същи и за двете к-ни системи, но понеже в условието не разполагаш с дължината и ширината, трябва да ги изчислиш на основата на горния ляв и долния десен ъгли. По-конкретен пример е следното изображение (само с линк, защото е твърде голямо). На него също разполагаме с правоъгълник, и неговия горен ляв ъгъл има координати (1, 1), докато долния десен ъгъл има координати (5, 3). Дължината и ширината на този правоъгълник ще намерим след като съобразим, че те съвпадат с разстоянията от дадените съответни върхове на правоъгълника, което означава, че работим със стойностите по оста X и Y. Това налага изваждането на x и y координатите на двете точки, но в същото време трябва да помним и, че от математическо и логическо гледище, стойността на ширината - както и на дължината - не може да бъде отрицателно число. Затова и в изразите използваме Abs() (абсолютната стойност на дадено число, която е винаги положителна). Останалото е праволинейно приложение на фолмулите за лице и периметър на правоъгълник.

19/01/2017 19:36:56

fbinnzhivko 1586 Точки

Колега даи линкове към задачите в Judje или условията или твои код във paste.bin.
Повече хора биха ти помогнали по този начин.

19/01/2017 18:07:35

louche 3 Точки

Мислех си го, но не исках да ангажирам с конкретно решение. Иначе:

2/8

      double x1 = Double.parseDouble(console.nextLine());
      double y1 = Double.parseDouble(console.nextLine());
      
      double x2 = Double.parseDouble(console.nextLine());
      double y2 = Double.parseDouble(console.nextLine());
      
      double width = Math.abs(x1 - x2);     
      double height = Math.abs(y1 - y2);
      
      double area = width * height;
      double perimeter = 2* (width + height);
      
      System.out.println(area);
      System.out.println(perimeter);

4/3

      Scanner console = new Scanner(System.in);
      double x1 = Double.parseDouble(console.nextLine());
      double y1 = Double.parseDouble(console.nextLine());
      
      double x2 = Double.parseDouble(console.nextLine());
      double y2 = Double.parseDouble(console.nextLine());
      
      double x = Double.parseDouble(console.nextLine());
      double y = Double.parseDouble(console.nextLine());
      
      if ((x >= x1 && x <= x2) && (y >=y1 && y <= y2)) {
        System.out.println("Inside");
      } else {
        System.out.println("Outside");
      }

4/6

        double x1 = Double.parseDouble(console.nextLine());
        double y1 = Double.parseDouble(console.nextLine());

        double x2 = Double.parseDouble(console.nextLine());
        double y2 = Double.parseDouble(console.nextLine());

        double x = Double.parseDouble(console.nextLine());
        double y = Double.parseDouble(console.nextLine());

        boolean isOnLeftSide = (x == x1) && (y >= y1 && y <= y2);
        boolean isOnRightSide = (x == x2) && (y >= y1 && y <=y2);
        boolean isOnTopSide = (y == y1) && (x >= x1 && x <= x2);
        boolean isOnBottomSide = (y == y2) && (x >=x1 && x <= x2);

        if (isOnLeftSide || isOnRightSide || isOnTopSide || isOnBottomSide) {
            System.out.println("Border");
        } else {
            System.out.println("Inside / Outside");

19/01/2017 18:10:10 19/01/2017 19:08:37

fbinnzhivko 1586 Точки

Задачата за rectangle e много добре обяснена тук

Задача 2.Имаш 4 boolen променливи.
Искаш да провелиш дали търсената точка лежи на някои от тези 4 страни.

boolean isOnLeftSide = (x == x1) && (y1<= y && y <= y2);
Търсената точка лежи на лявата част на правоъгълника ако x на търсената точка е равен x на лявата страна на правоъгълника (x == x1) и y на търсената точка е по малък или равен от y на горния ляв ъгъл на правоъгълника (y <= y2)и y на търсената точка е по голям или равен от y на долния ляв ъгъл на правоъгълника(y1<= y).
За другите 3 страни е същотото.
Накрая проверяваш дали една от тези 4 проверки е изпълнена isOnLeftSide || isOnRightSide || isOnTopSide || isOnBottomSide.Ако една е изпълнена лежи на една от 4 страни.
Ако никоя от тези проверки не е изпълнена точката лежи вътре или извън правоъгълника.

19/01/2017 19:05:03 19/01/2017 19:26:11

ThePSXHive 436 Точки

Относно задачите с допълнителните логически проверки, можем да се върнем към инвертираната координатна система и да разгледаме един пример с две точки в равнината - едната извън, а другата вътре в даден правоъгълник:

Точката P е вътре в правоъгълника, докато точката O е извън него. Разликата е, че координатите на точката P са ограничени от координатите на правоъгълника, и с първата част на проверката за "вътрешност/външност" искаме да се уверим, че стойността на абцисата (стойността по оста X) на точка P е ограничена от стойността на координатите на правоъгълника. Първата част от проверката изглежда така

(x >= x1 && x <= x2)

В случая, стойността на x e 200 (виж точка P отново), a стойностите на x1 и x2 са съответно 40 и 280 (виж горния ляв и долния десен ъгъл на правоъгълника). Като заместим тези стойности ще получим

200 > 40 && (И) 200 < 280

Понеже тази проверка е вярна (стойността и е истинна, защото заместването действително удовлетворява условието), преминаваме към втората част и разсъждаваме по аналогичен начин. Ако ординатната стойност на P (стойността по оста Y) е ограничена от правоъгълника, то и двете проверки са верни, и точката е вътре. Разбира се, тези проверки не са истинни за точката O, която не е ограничена от координатите на правоъгълника. В другата задача разсъждаваме по същия начин, но там се отчита и фактът, че една от координатите на точката съвпада с една от координатите на два от върховете на правоъгълника.

19/01/2017 20:13:55

louche 3 Точки

Изключително много ти благодаря за отделеното време и подробните разяснения!

20/01/2017 11:56:56 20/01/2017 11:58:13